They are classes that describe how hard a problem is.
Imagine trying to explain to someone how fast you can do something, for example sorting a list. The simplest way would be saying “I can do that in two seconds” but that’s not very helpful because it depends on how fast your computer is. A better way would be to express it as a number of steps: “I can do that in 10000 steps”. For this ELI5 explanation the exact definition of what a step is doesn’t matter that much, it could be a single CPU instruction or a comparison between two items in the list.
That gets you a bit closer but obviously, how complex sorting a list is, depends on the list: how long is it and how scrambled is it? Short lists are faster to sort than long ones and lists that are already (almost) sorted are usually fasterto sort than ones in reverse or completely random order. For that you can say “In the worst case, I can sort a list in three times the number of items squared, no matter the initial order”. When writing that down, we call the number of items
n, so the total work is3 * n^2. The biggerngets, the less the constant factor matters, so we can leave it out and instead writeO(n^2). This is, what people call “Big O notation” and it’s the reason why I said the exact definition of a step doesn’t matter that much. As long as you don’t get it too wrong, different step definitions just change the constant that we’re ignoring anyway. Oh and by the way,O(n^2)for sorting lists isn’t that great, good algorithms can reachO(n*log(n))but I didn’t want to throw logarithms at you right away.Now we get close to understanding what P is. It’s the class of all problems that can be solved in “polynomial” time, so
O(n^a)for any numbera. Note that only the highest exponent is relevant. With some work we could prove that for exampleO(n^3 + n^2 + n)is equivalent toO(n^3). Examples of problems innare sorting, route planning and finding out if a number is prime.I’m running out of time because I have some errands to run, maybe someone else can explain NP (nondeterministic polynomial time). If not, I’ll add a follow up later today.
Alright, part 2, let’s get to NP.
Knowing that P means “in polynomial time”, you might be tempted to think that NP means “in non-polynomial time” and while that kind of goes in the right direction, it means “in non-deterministic polynomial time”. Explaining what non-deterministic calculations are would be a bit too complicated for an ELI5, so let’s simplify a bit. A regular computer must make all decisions (for example which way to turn when calculating a shortest route between two points) based on the problem input alone. A non-deterministic computer can randomly guess. For judging complexity, we look at the case where it just happens to always guesses right. Even when guessing right, such a computer doesn’t solve a problem immediately because it needs to make a number of guesses that depends on the input (for example the number of road junctions between our points). NP is the class of problems that a non-deterministic computer can solve in polynomial Time (
O(n^a)for any a).Obviously, we don’t really have computers that always guess right, though quantum computers can get us a bit closer. But there are three important properties that let us understand NP problems in terms of regular computers:
- a non-deterministic computer can do everything a regular computer can do (and more), so every problem that’s part of P is also part of NP.
- every problem that takes
nguesses withxoptions for each guess can be simulated on a regular computer inO(x^n)steps by just trying all combinations of options and picking the best one. With some math, we can show that this is also true if we don’t havenbutO(n^a)guesses. Our basexmight be different, but we can always find something withnin the exponent. - While finding a solution on a regular computer may need exponential time, we can always check if a solution is correct in polynomial time.
One important example for a problem in NP is finding the prime factors of a number which is why that is an important basic operation in cryptography. It’s also an intuitive example for checking the result being easy. To check the result, we just need to multiply the factors together and see if we get our original number. Okay, technically we also need to check if each of the factors we get is really prime but as mentioned above, that’s also doable in polynomial time.
Now for the important thing: we don’t know if there is some shortcut that lets us simulate NP problems on a regular computer in polynomial time (even with a very high exponent) which would make NP equal to P.
What we do know is that there are some special problems (either from NP or even more complex) where every single problem from NP can be rephrased it as a combination of that special problem plus some extra work that’s in P (for example converting our inputs and outputs to/from a format that fits L). Doing this rephrasing is absolutely mind-bending but there are clever computer scientists who have found a whole group of such problems. We call them NP-hard.
Why does this help us? Because finding a polynomial-time solution for just a single NP-hard problem would mean that by definition we can solve every single problem from NP by solving this polynomial-time NP-hard problem plus some polynomial-time extra work, so polynomial-time work overall. This would instantly make NP equal to P.
This leaves us with the definition of NP-complete. This is simply the class of problems that are both NP-hard and themselves in NP. This definition is useful for finding out if a problem is NP-hard but I think I’ve done enough damage to your 5-year-old brain.
One important addendum: complexity classes always consider how hard a problem is depending on the input size. Sorting is in P (usually
O(n*log(n)), so one of the easiest problems overall) but given a few trillion inputs, it would be pretty much impossible to solve on consumer hardware. On the other hand, problems like 3-sat, the knapsack problem or travelling salesman are all NP-hard but with small enough inputs (up to a few dozen or so), they are easy to solve, even with pen and paper and are even regularly included in puzzle books.I had a huge reply, but after some googling to try and understand, I’m gonna go with this wiki image:
(Black graph on transparent background, this might be better: https://en.m.wikipedia.org/wiki/NP_(complexity)#/media/File%3AP_np_np-complete_np-hard.svg )
I see it as:
P: is a problem that gets solved and proved easily.
Np: is is a problem that is difficult to solve but easy to prove.
P=np ie np-complete: as difficult to solve as it is to prove.
Np-hard: no single solution, might require multiple “np” solutions (eg a different algorithm for each input element)The diagram is pretty good but your interpretation is not quite right, especially for NP-complete and NP-hard.
NP-hard means “at least as hard as all problems in NP”, proven by the fact that any single NP-hard problem can be used to solve the entire class of all NP problems.
NP-complete means “at least as hard as all problems in NP and itself also in NP”, so the intersection between NP and NP-hard.
The thing about P = NP or P != NP is something different. We don’t know if P and NP are the same thing or not, we don’t have a proof in either direction. We only know that P is at least a subset of NP. If we could find a P solution for any NP-hard problem, we would know that P = NP. That would have massive consequences for cryptography and cyber-security because modern encryption relies on the assumption that encrypting something with a key (P) is easier than guessing the key (NP).
On the other hand, at some point we might find a mathematical proof that we can never find a P solution to an NP-hard problem which would make P != NP. Proving that something doesn’t exist is usually extremely hard and there is the option that even though P != NP we will never be able to prove it and are left to wonder for all eternity.
That was awesome, thank you!
Note that only the highest exponent is relevant. With some work we could prove that for example
O(n^3 + n^2 + n)is equivalent toO(n^3).just adding on for others that “some work” can be simply explained as figuring out the answer to “as
ngrows, which of n3, n2 or n affects the result the most?”Yes, it’s pretty intuitive. A formal proof is still a bit more work than what I can fit in an ELI5 but at the same time simple enough that it can be given to a 2nd semester computer science student as an exercise.
That’s a great write up! I’d love to read part 2
Done.
This is a pretty good summary of the classes of algorithms and an open problem related to them:
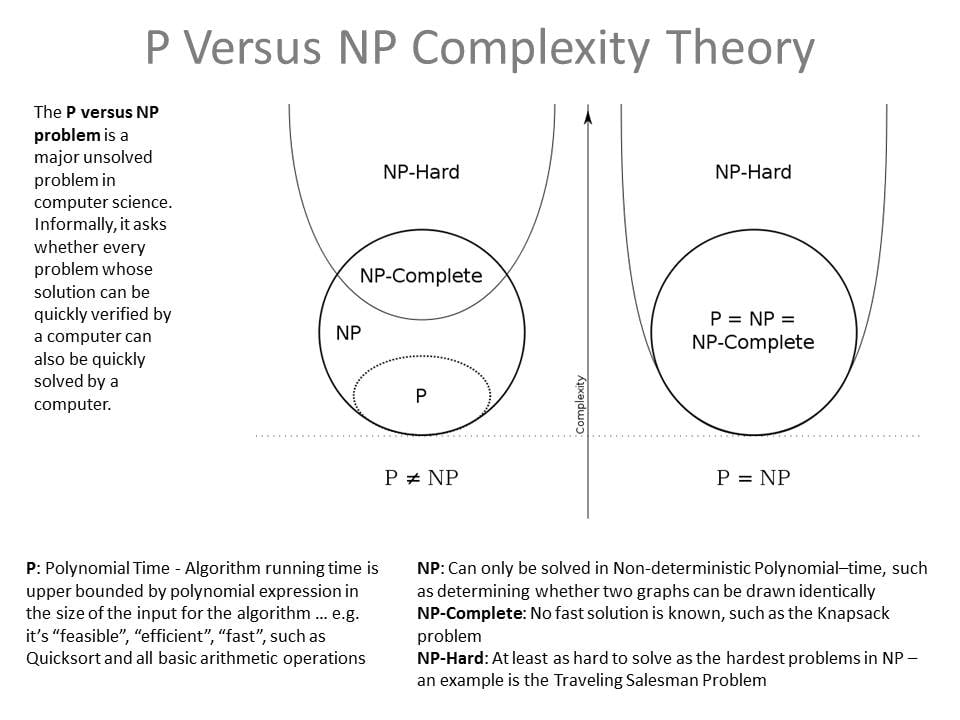
Alt: diagrams showing from P to NP-Hard under p=np and p!=np models, with a brief description of each and an example of each.
Great summary; thank you
Some computing problems are “easy”* to solve. We call these P.
Some problems let us easily check a proposed solution if we’re given one. We call these NP.
All problems in P are also in NP, since checking a solution proposal works is never harder than solving the problem starting from nothing.
We suspect but can’t prove that some problems in NP are not in P.It turns out that it’s possible to translate any problem in NP into the boolean satisfiability problem (SAT) using an easy algorithm, so this problem effectively is an upper bound on how hard it could be to solve problems in NP - we could always translate them into SAT and solve that instead if that sequence is easier.
We call SAT, and any problem that it can be translated into easily in the same way, the problem class NP-hard.
NP-complete is just those NP-hard problems which are also in NP, which is many but not all of them.*: require asymptotically polynomial running time
Some problems get harder to do on bigger numbers. Like breaking a number into factors; the bigger the number, the harder it is to find the factors. Contrast this with, say, telling whether the number is even, which is easy even for very very large numbers.
There is a certain measure of how quickly problems get harder with bigger numbers called Polynomial Time; this is the P in P, NP, etc. I will omit the details of what polynomial time means exactly because if you don’t know from the name, then the details aren’t particularly important. It’s just a certain measure of how quick or hard the problem is to solve.
So for the various types of problems:
- P - The list of problems that can be solved quickly. For example, telling if a number is even.
- NP - The list of problems where you can check the answer quickly. For example, factoring a number.
- NP Complete - A list of special NP problems where we know how to “translate” any NP problem into one of these NP complete problems. Solving a Peg Solitaire game is NP complete.
- NP Hard - Problems at are as hard as NP Complete or harder. The travelling salesman problem (finding the shortest route that visits a list of cities) and the halting problem (figuring out if a computer program will get stuck in an infinite loop) are NP Hard.
I can only explain P, NP, and, NP-complete since those are on my exam. Firstly, P and friends are “sets” meaning they hold a collection of something. In this case it is the set of all problems that satisfy certain properties. A problem is something that requires an algorithm to reach a solution for any input. An algorithm is a protocol to complete some sort of procedure… it’s a series of steps. What’s important in P and NP is the number of steps this algorithm completes relative to the input size. We call this runtime. For example, n^2 is polynomial runtime, because as the input grows, the runtime grows exponentially. If the runtime is exponential, like 2^n, then it seemingly doubles or triples every time you increase the input - which for all things computer, is not nice. Any problem that has a known algorithm already to find a solution efficiently (in polynomial time) is in P. If the problem doesn’t, then it may be in NP. If a problem has an efficient “verifier” or something that can take a problem, its input, its solution, and “verify” that the solution is correct for all inputs, then it is in NP. However, this verifier has to be efficient. If something is in NP then we know of a sanity check to test if our solution from some kind of magic and otherworldly algorithm is correct. Naturally, if something is in P, it is also going to be in NP - but I think that’s because the algorithm is only returning true or false, which are called decision algorithms. An example would be: can I color this graph with 3 colors so that two nodes on an edge have different colors?
Lastly, the concept of “polynomial reducibility” becomes relevant. Basically, mathematicians think there is some sort of invisible problem out there that is represented by NP Complete. Like, the Question to all Life, the Universe, and Everything. The reason they think this is because quite a lot of problems seem to be the same problems. As in - rephrasing another problem brings you to another problem you’re familiar with. This is important since if you’re trying to find an efficient algorithm to X and know Y is “the same problem” then find an algorithm to Y, well, you’ve found an algorithm for X too. Since our algorithm has to be “efficient” or polynomial, something is reducible if there is a sort of pre-processing and post-processing step to convert an input to X to an input for Y in polynomial time. The common analogy is that Y is a black box, it computes an answer but can only speak a certain language. So, you translate your native language (problem X) to its language (problem Y), let it compute its answer, then translate its response back.
What this boils down to is, NP-complete is a class of problems to which there isn’t a readily available efficient algorithm for any of them, since they’re all the same NP problem essentially, and finding an algorithm to one means you find one to all of them. NP-C contains quite a lot of problems and most are seemingly unrelated. However, since no algorithm has been found to solve any efficiently, it might seem that none exists. Therefore, if you discover that an NP problem you’ve been so enthusiastically working on a solution for is polynomially reducible to something in NP complete, you should just give up, because other smarter and more talented people have already given a crack at it and failed.
This video helped me get questions relating to P vs NP correct in my Complexity and Computation undergrad class.
#/media/File%3AP_np_np-complete_np-hard.svg){kind=link}